A problem we see in psychological network papers is that authors sometimes over-interpret the visualization of their data. This pertains especially to the layout and node placement of the graph, for instance: do nodes in the networks cluster in certain communities.
Below I will discuss this problem in some detail, and provide a basic R-tutorial on how to identify communities of items in networks. You can find the data and syntax I use for this tutorial here — feedback is very welcome in the comments section below.
Node placement and the Fruchterman-Reingold algorithm
Let’s create an example so we can see what the challenge is. First, we take some data I happen to have lying around, estimate a regularized partial correlation network where the edges between nodes are akin to partial correlations, and plot the network, using the layout='spring' command. This is the default in the psychological network literature, and uses the Fruchterman-Reingold algorithm to create a layout for the nodes in the graph: nodes with the most connections / highest number of connections are put into the center of the graph.
library("qgraph")
load("data.Rda")
cormatrix <- cor_auto(data)
graph1<-qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),
vsize=7, cut=0, maximum=.45, border.width=1.5) |
cormatrix is simply the correlation matrix of the 20 items, and the sampleSize command tells R how many people we have. The bottom line makes the graph pretty. 😉
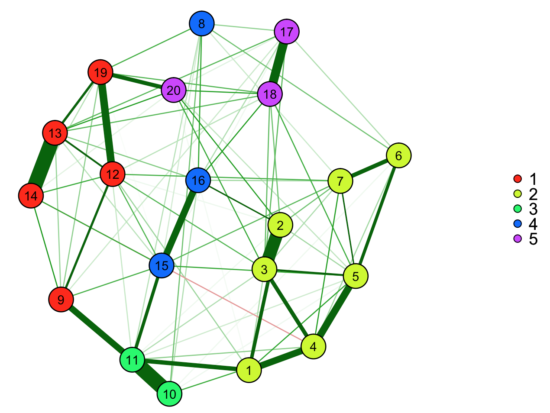
This is the resulting figure:
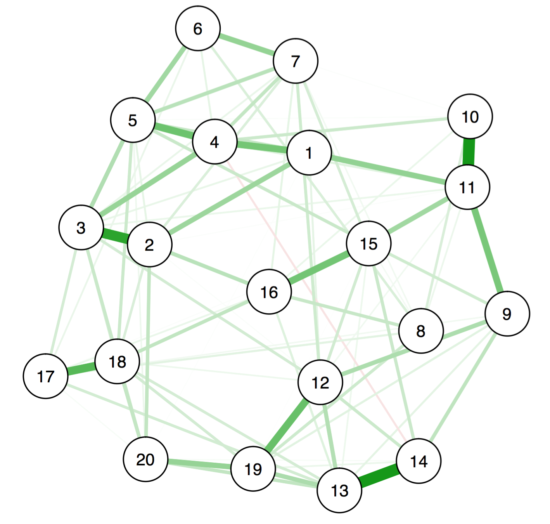
However, the node placement here is just one of many equally ‘correct’ ways to place the nodes. When there are only 1-3 nodes in a network, the algorithm will always place them in the same way (where the length of the edges between the nodes represent how strongly they are related), and the only degree of freedom the algorithm has is the rotation of the graph. But especially in graphs with many nodes, the placement tells us only a very rough story, and should not be over-interpreted.
Here are two more ways to plot our above network that are equally ‘correct’.
nNode <- 20
set.seed(1)
graph2<-qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),
vsize=7, cut=0, maximum=.45, border.width=1.5, layout.par = list(init = matrix(rnorm(nNode*2),nNode,2)))
set.seed(2)
graph3<-qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),
vsize=7, cut=0, maximum=.45, border.width=1.5, layout.par = list(init = matrix(rnorm(nNode*2),nNode,2))) |
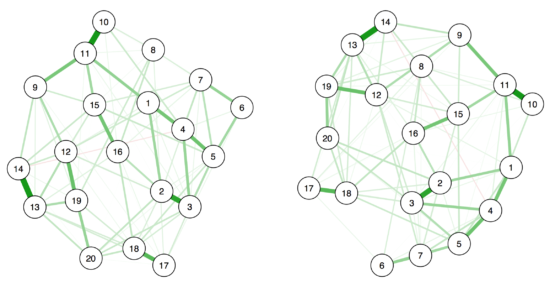
While the edges between items are obviously the same, the placement of the nodes differs considerably.
Madhoo & Levine 2016
A new paper by Madhoo & Levine (in press) in European Neuropsychopharmacology provides a good example for this challenge. They investigated the networks structure of 14 depression symptoms in about 2500 psychiatric outpatients diagnosed with Major Depression at two timepoints (12 weeks apart). A very cool contribution of the paper is that they examined the change of the network structure over time, in a somewhat different way than we did previously in the same dataset.
Similar to the network example above, they used regularized partial correlation networks to estimate the cross-sectional network models at both timepoints, and plotted the networks using the Fruchterman-Reingold algorithm. They concluded from visually inspecting the graphs that there are 4 symptom clusters present, and that these did not change over time:
“At baseline the network consisted of four symptom groups (Figure 1a) of: Sleep disturbances (items 1–5), cognitive and physical avolition (items 6–9), Affect (items 10–12) and Appetite (items (13–14).
[…]
The endpoint symptoms groupings (in Figure 1b) resembled that at baseline”.”
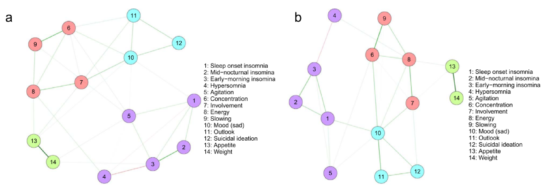
But these findings and conclusions are merely based on visual inspection of the resulting graphs — and has we have learned above, these should be interpreted with great care. Of note, this visual over-interpretation is pretty common in the psychological network literature, and I really don’t want to call out Madhoo & Levine specifically for their great paper; it just happens to be the most recent example that came across my desk.
Another reason why this stood out to me is that we have analyzed the community structure in the same dataset in a recent paper, and found that the number of communities changes over time — which conflicts with the authors’ visual interpretation of the graphs.
Data-driven item clustering in R
So what might be a better way to do this, and how can we do it in R? There are numerous possibilities, and I introduce three: one very well-established method from the domain of latent variable modeling (eigenvalue decomposition); one well-established algorithm from network science (spinglass algorithm); and a very new tool that is under development (exploratory graph analysis which uses the walktrap algorithm).
Eigenvalue Decomposition
Traditionally, we would want to describe the 20 items above in a latent variable framework, and the question arises: how many latent variables do we need to explain the covariance among the 20 items? A very easy way to do so is to look at the eigenvalues of the components in the data.
plot(eigen(cormatrix)$values, type="b") abline(h=1,col="red", lty = 3) |
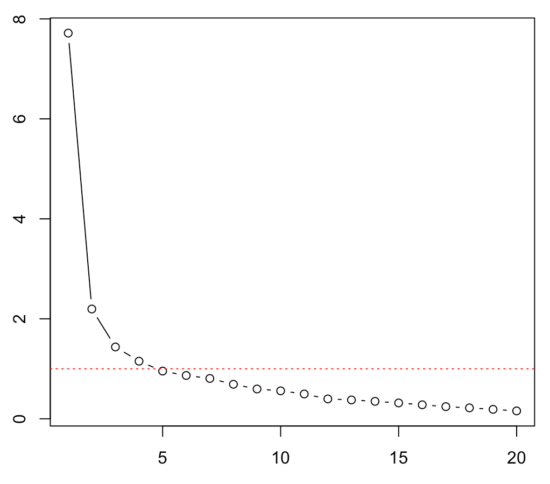
This shows us the value of each eigenvalue of each components on the y-axis; the x-axis shows the different components. A high eigenvalue means that it explains a lot of the covariance among the items. The red line depicts the so-called Kaiser criterion: a simple rule to decide how many components we need to describe the covariance among items sufficiently (every components with an eigenvalue > 1). There are better ways to do so, such as parallel analysis, which you can also do in R. In any case, depending on the rule we use now, we would probably decide to extract 2-5 components. We do not yet know what item belongs to what component — for that, we need to run, for instance, an exploratory factor analysis (EFA) and look at the factor loadings. And yes, you guessed correctly: you can obviously also do that in R … life is beautiful! 😉
Why is this related to networks at all? Numerous papers have now shown that latent variable models and network models are mathematical equivalent, which means that the numbers of factors that underlie data will in most cases translate to the number of communities you can find in a network.
Spinglass Algorithm
A second method is the so-called spinglass algorithm that is very well established in network science. For that, we feed the network we estimated above to the igraph R-package. The most relevant part is the last line sgc$membership.
library("igraph")
g = as.igraph(graph1, attributes=TRUE)
sgc <- spinglass.community(g)
sgc$membership |
In our case, this results in “5 5 5 5 5 5 5 2 3 1 1 3 3 3 4 4 2 2 3 3”. This means the spinglass algorithm detects 5 communities, and this vector represents to which community the 20 nodes belong (e.g., nodes 1-7 belong to community 5). We can then easily plot these communities in qgraph by, for instance, coloring the nodes accordingly. Note that iqgraph is a fantastically versatile package that has numerous other possibilites for community detection apart from the spinglass algorithm, such as the walktrap algorithm. (Thanks to Alex Millner for his input regarding igraph; all mistakes here are my mistakes nonetheless, of course).
It is important to note that the spinglass algorithm will often lead to different results every time you run it. This means you should set a seed via set.seed() before you run spinglass.community, unlike I do above. I often run the algorithm 1,000 times, look at the median number of clusters that I obtain, and then find a seed which reproduces this median number of clusters. I use this solution for a paper (noting that solutions look different with a different seed)1
It is also crucial to know that there are many dozens of different ways to do community detection. Spinglass is somewhat simplistic because it only allows items to be part of one community — but it could be that items are better described as belonging to several communities at the same time. Barabási’s book “Network Science” has an extensive chapter on community detection (thanks to Don Robinaugh for the tip). Spinglass is just one of many opportunities. As I mentioned above: walktrap, for instance, is also commonly used, and much more stable, i.e. more likely to find the exact same resolution if you repeat it, unless you go for very long random walks.
Exploratory Graph Analysis
The third possibility is using Exploratory Graph Analysis via the R-package EGA that is currently under development. This means you really want to check what is happening and make sure you trust the package before you publish a paper using its results, but the preprint looks promising2. This package re-estimates a regularized partial correlation network from your data, similar to what we have done above, and then uses the walktrap algorithm to find communities of items in your network. This should lead to identical results compared to igraph in case the walktrap algorithm is used (and the details are set equally, such as the number of steps).
The advantage of EGA is that — unlike eigenvalue decomposition — it shows you directly what items belong to what clusters. The author of the EGA package is currently testing the performance of different ways to detect communities (see this paper for more details on the topic).
library("devtools")
devtools::install_github('hfgolino/EGA')
library("EGA")
ega<-EGA(data, plot.EGA = TRUE) |
If the method turns out to work well, it’s very easy to use and automatically shows you to which communities your items belong.
Note that at present, EGA takes your data and automatically estimates a Gaussian Graphical Model (that assumes multivariate normal variables). If you have binary data, they do not fulfil the assumptions to estimate such a model. I hope that EGA in the future will be adapted to estimate the Ising Model for binary data which is the appropriate regularized partial correlation model for such data (ref1, ref2).
Do EGA and spinglass give us the same results?
Update: I added this section after a comment by KSK below. Now, we want to check our results for robustness: do the igraph spinglass algorithm and EGA which uses the walktrap algorithm agree in their community detection?
That’s pretty easy to do: let’s plot the two networks next to each other and color the communities accordingly. First, we define the communities based on the EGA and igraph results, and then plot the networks using the layout of the very first network above.
group.spinglass<- list(c(1:7), c(8,17,18), c(9,12,13,14,19,20), c(10,11), c(15,16))
group.ega<- list(c(1:7), c(8,15,16), c(10,11), c(17,18,20), c(9,12:14,19))
par(mfrow = c(1, 2))
graph4 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.ega,
vsize=7, cut=0, maximum=.45, border.width=1.5,
color=c("red", "green", "blue", "orange", "white"), title="ega walktrap")
graph5 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.spinglass,
vsize=7, cut=0, maximum=.45, border.width=1.5,
color=c("red", "orange", "white", "blue", "green"), title="igraph spinglass") |
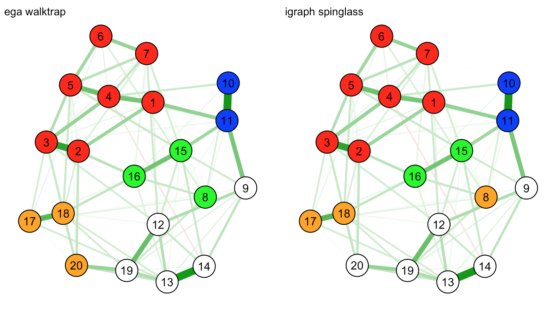
Intuitively — based on visual inspection — the EGA solution seems to make more sense, where node 8 belongs to the green community instead of the orange one. But, again, this is just a graphical display of complex relationships, and we must be careful with interpretation here.
So let’s plot the same network with a slightly different (random!) layout; again, this layout is not better or worse than the layout above:
par(mfrow = c(1, 2))
set.seed(5)
graph4 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.ega,
vsize=7, cut=0, maximum=.45, border.width=1.5,
color=c("red", "green", "blue", "orange", "white"), title="ega walktrap",
layout.par = list(init = matrix(rnorm(nNode*2),nNode,2)))
set.seed(5)
graph5 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.spinglass,
vsize=7, cut=0, maximum=.45, border.width=1.5,
color=c("red", "orange", "white", "blue", "green"), title="igraph spinglass",
layout.par = list(init = matrix(rnorm(nNode*2),nNode,2))) |
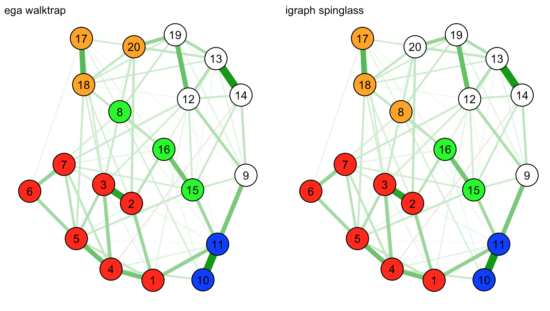
As you can see now, in this visualization it is unclear whether node 8 should belong to the green or orange communities, and we have no clear intuitive favorite.
Conclusions
If you are interested in statistical communities among items in your network, please do more than visually inspect your graph. When I do this for papers, I use the three methods described above, and usually they result in fairly similar findings. Obviously, it may also be that you are more interested in theoretical or conceptual communities. In that case, you may not need to look at your data at all, and all is well without going through all the above trouble.
Note that the biggest limitation of the community detection methods such as spinglass or walktrap described above is that items deterministically belong to one community only. For psychological data, where fitting a factor model often identifies items that have cross-loadings, this is an issue. And you can see that by simulating from a 2 factor model where 1 item loads equally well on both factors: repeating spinglass over and over will show that the item switches membership. Hopefully, we will soon have algorithms implemented in R that allow items to belong to multiple communities at the same time (Barabási describes several in chapter 9 of his Network Science book.
Update October 2017
The spinglass algorithm can give fairly different results if you run it multiple times, while the walktrap algorithm is fairly deterministic. You can use this loop if you are interested to see how spinglass results differ over, for instance, 100 repetitions.
network1 < - estimateNetwork(data1, default="IsingFit")
graph1 < - plot(network1)
g = as.igraph(graph1, attributes=TRUE)
matrix_spinglass < - matrix(NA, nrow=1,ncol=100)
for (i in 1:100) {
set.seed(i)
spinglass < - spinglass.community(g)
matrix_spinglass[1,i] < - max(spinglass$membership)
}
mean(as.vector(matrix_spinglass)) #5.87
max(as.vector(matrix_spinglass)) #7
min(as.vector(matrix_spinglass)) #5
median(as.vector(matrix_spinglass)) #6 |
The comments below provide answers to some additional questions and may be worth checking out, e.g., the comparison of different algorithms in the same data.
- Update November 2017: Note that it might be useful to investigate the stability of the clustering solution on different levels; a student I work with has had a few great ideas in that regard, and I will update the tutorial once more information is available.
- Update November 2017: This is published now, and Hudson added a very cool plotting option recently! Definitely worth checking out.
Cool! I’d like to add that you can use averageLayout to obtain a layout based on two networks:
Layout <- averageLayout(graph1, graph2)
Which you can then use in qgraph:
qgraph(…, layout = Layout)
It's always advisable to plot two networks of the same nodes with the same layout, to avoid above mentioned interpretation problems.
That’s really cool!!
Nice!
A couple of questions about the EGA results. What is the reason node 8 is getting assigned to the same community as nodes 15 and 16 (rather than the community in green or magenta)? Why isn’t node 9 assigned to the green community instead of the red? I can only imagine that if I would 3D print the relations instead of 2D (so the result would be ballish instead of circleish) that 9 is closer (on average) to the other red dots than to the green dots, although the edges suggest otherwise. In any case, I was wondering if the danger of visually inspecting a 2D graph of higher (n) dimensional relations lies in the n-D to 2-D reduction. If so, what is the benefit of a graphical method over, say, a table of pca factor loadings? Or a path diagrammatical representation of such a table? (feasible with this relatively small number of nodes).
Or did the assignment have to do with the difference between zero-order correlations versus partial correlations? I know you’re a proponent of inspecting partial correlations, so I assumed the plot might be based on partial correlations while the EGA provides information on zero-order correlations or the other way around. Can you clarify the nature of the correlations?
Based solely on my own (lack of) visualization skills I would have clustered differently. But usually I tend to play around with the arguments in qgraph to get an idea of how sensitive or robust the clustering is towards the values of those arguments, including the choice of the algorithm. (so thanks for the averaging tip, Sacha!)
Good points, thanks. I’ll answer here and then maybe edit the post above to clarify.
1) EGA estimates a gaussian graphical model with regularization, using what we believe to be the most reliable defaults at the moment (cor_auto to get the covariance matrix, then GGM with standard regularization tuning parameter of 0.5). This is exactly what I did in the example above, and hence will lead exactly to the same network structure. If I were to take the output from EGA and plot it in qgraph, using the same graphical arguments and layout above, it would be identical.
2) You summed up the problem much better than I did: n-D to 2-D reduction. And yes, multiple people in the last years have actually called for avoiding graphs altogether, and plotting tables instead. I think we should do both, because both provide different answers. Personally, if I have to choose, I’d rather have a visualization of the table when I know how to interpret it, rather than a 20×20 table that has mostly 0s and is rather difficult to figure out by just looking at it.
3) Different clustering: EGA uses the walktrap algorithm and is under development, and it usually gives me slightly different results than igraph with the spinglass algorithm. Let’s check it out in this case, actually.
Not sure how formatting works in comments … let’s see. Here is the rcode. I define groups based on the 2 community analyses outputs:
# spinglass: 5 5 5 5 5 5 5 2 3 1 1 3 3 3 4 4 2 2 3 3sgc$membership
# ega: 2 2 2 2 2 2 2 4 1 3 3 1 1 1 4 4 5 5 1 5ega$wc
group.spinglass<- list(c(1:7), c(8,17,18), c(9,12,13,14,19,20), c(10,11), c(15,16))group.ega<- list(c(1:7), c(8,15,16), c(10,11), c(17,18,20), c(9,12:14,19))
Then we estimate the 2 networks; I simply use the layout of our very first graph.
graph4 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.ega, vsize=7, cut=0, maximum=.45, border.width=1.5, color=c("red", "green", "blue", "orange", "white"))graph5 <- qgraph(cormatrix, graph="glasso", layout="spring", sampleSize = nrow(data),groups=group.spinglass, vsize=7, cut=0, maximum=.45, border.width=1.5, color=c("red", "orange", "white", "blue", "green"))Result:
You can see that node 8, again, is somewhat problematic. I would assume that in a factor model, it would either have no loadings on any of the 5 factors, or cross loadings between several.
Now, I played around with different seeds to plot this graph, and after 3 tries I discovered this plot:
Here you see exactly why we should not overinterpret these graphs .. in this 2d renditon of the n-d data, the 2 different community detection algorithms both make equal sense, while they do not in the first plot above.
Good points! I have a few comments:
Personally, I think visually inspecting the result of cluster (or community) detection in networks very insightful. However, I don’t think the visualization per se is the final goal when a person uses, for example, EGA. The goal, or at least my goal, when I use EGA is try to discover the dimensionality of a given instrument. So, if the EGA results in 4 communities, we can verify if this first-order structure fits the data, via confirmatory factor analysis. In the EGA package I have implemented a function, called CFA, that uses the structure suggested by EGA and runs a CFA. My experience shows that, in general, the fit is very good (CFI > .95 and RMSEA < 0.05). So, what are the advantages of investigating dimensionality via EGA and related methods (i.e. via community detection in regularized partial correlation networks)? 1) It shows you which item belong to each dimension, 2) allow an easy inspection of model fit, via CFA, 3) can be used to investigate, for example, the stability of the structure via bootstrap (in the EGA package we have the bootEGA function). One may argue that “networks are totally different from latent variable models, so why to use CFA from a structure found via some network strategy?” Well… it seems that in some specific cases, network models and latent variable models are two sides of the same coin…
Furthermore, as far as our simulations show (see arxiv.org/abs/1605.02231), using EGA to investigate the dimensionality of an instrument can be as good as, and in some cases, more accurate than traditional methods as parallel analysis, Kaiser-Guttman’s eigenvalue rule and so on.
Minor freudian typo: “we estimated already to the iqgraph R-package” (and the following code misses a quote mark). Thanks for the post, these tutorials are much needed!
I read through it 5 times and didn’t see it! That’s how often I’ve written “qgraph” in the last years 😉 … thanks for pointing out the 2 mistakes Matti.
Thank your for this tutorial, very useful! I think this way to analyze psychometric tests is promising. I would like to report a problem in the code. Describing the usage of the spinglass algorithm with igraph, you build the function “community.newman”, but you use the function “spinglass.community”.
Thanks for finding this error Davide, the function
community.newmanisn’t actually needed, so you can ignore that part of the code (and I’ll delete it from the post and code).Just a brief question: I think it would be a good idea to take the stochastic nature of the spinglass algorithm into account when interpreting its results – they will change from one iteration to the other.
Hi Markus, what do you mean with iteration? The network structure is always the same, just the visualization is different.
Thanks for sharing this Eiko! it was indeed very helpful.
Just a question, and perhaps it is not relevant to your post, but I am trying to use the same layout (nodes at the same position) for three different networks. I have the 1) network of the entire sample, 2) network of the boys only, and 3) network of the girls only. I was wondering if you could so kindly advise what code i should use to generate the same layout for all 3? Many thanks in advance for your help!
Hi Amy.
You estimate the three networks, let’s say
g1 <- qgraph(data1, layout="spring", ...)g2 <- qgraph(data2, layout="spring", ...)g3 <- qgraph(data3, layout="spring", ...)Then:
L <- averageLayout(getWmat(g1), getWmat(g2), getWmat(g3))This averages the layout of the 3 adjacency matrices (the command is slightly different if you have an Ising model instead of a Gaussian Graphical Model).
And then you plot the graphs again with layout=L (either using qgraph() or plot() ).
plot(g1, layout=L)plot(g2, layout=L)plot(g3, layout=L)Let me know if this works for you!
EDIT: there shouldn't be a space between <-, can't get it to work properly on my phone right now sorry.
No worries, thanks so much for the quick reply Eiko!
I just had a try, and it did not work. I applied EBICglasso to the GGM model.
Would that have made things different? here is what i did with EBICglasso for the girls only data as an example (I did the same for boys only and the full data):
graph_girls.m <-EBICglasso(data_girls.cor, n = nrow(data_girls))
graph_girls.g<-qgraph(data_girls.cor, labels=names, directed=FALSE, graph="glasso", layout="spring", legend=TRUE, vsize=5.5, cut=0, maximum=.45, sampleSize = nrow(data_girls), border.width=2, border.color="black", minimum=.03, groups=groups, color=c('#bbbbbb','#a8e6cf', '#dcedc1', '#ffd3b6', '#ff8b94'))
then I followed your coding:
L<-averageLayout(getWmat(graph_facets.g), getWmat(graph_girls.g), getWmat(graph_boys.g))
plot(graph_facets.g, layout=L)
perhaps I did something wrong?
I just wrote this quickly for you. Use this as a template and you will get there. Note also that I use the new estimateNetwork() function from the new package bootnet() that will make your life easier. It looks terrible pasting it here, so I uploaded it here:
https://psych-networks.com/wp-content/uploads/2016/12/amy.txt
Thanks a lot, appreciate your help!
It worked, thanks so much!
Hi Eiko, thanks for sharing this averagelayout! it was indeed very helpful. I have tried use R code you provided to generate the same layout. Just a question, I am trying to change the color of edges in the network, but I always failed. How to add the R code in the previous R codes? Thank you for your consideration, I look forward to your early reply.
library(qgraph)
library(bootnet)
set.seed(1337)
x1<-rnorm(200)
x2<-rnorm(200)+0.5*x1
x3<-rnorm(200)+0.3*x2
set.seed(1337)
y1<-rnorm(200)
y2<-rnorm(200)+0.9*y1
y3<-rnorm(200)+0.1*y2
data1<-as.data.frame(cbind(x1,x2,x3))
data2<-as.data.frame(cbind(y1,y2,y3))
g1 <- estimateNetwork(data1, default="EBICglasso")
g2 <- estimateNetwork(data2, default="EBICglasso")
plot(g1, layout="spring", cut=0)
plot(g2, layout="spring", cut=0)
g1mat <- getWmat(g1)
g2mat <- getWmat(g2)
L <- averageLayout(g1mat, g2mat)
plot(g1, layout=L, cut=0)
plot(g2, layout=L, cut=0)
Hey, ?qgraph will show you how to change colors for edges, nodes, etc.
Eiko,
This is an excellent post (clearly I’m a bit behind on finding it), thank you so much. I had a short question for you regarding your suggestion to Amy. Will using the method you suggested to her create a sort of “averaged” Fruchtermam-Reingold layout that is no longer technically a Fruchterman-Reingold layout (but more of a “forced” layout? I am working on a psychopathy paper with multiple samples and the reviewers want the nodes to be in the same place for ease of comparison, and I am struggling between having supplementary graphs that just use a “circle” layout and using the method you specify here.
Thanks so much for these tutorials and any help!
Jon
Hi Jonathan, there is little you can do wrong here if you note the limitations. F-R has limitations, and one of them is that there are many layouts that describe the network equally well. But it does carry some information. Some papers have opted for circles to compare groups (e.g. 10.1001/jamapsychiatry.2015.2079), others for constrained F-R (e.g. 10.1016/j.drugalcdep.2016.02.005), and both are defensible.
I personally prefer constraining the layout of F-R to be equal in case there are considerable similarities across networks, using the averageLayout() function in R (e.g. https://osf.io/2t7qp/).
Thank you so much for the help. Two follow-ups that did not occur to me initially. If we used a short form of an instrument on one sample and the long-form on the other, does it make sense to do an average layout if the nnodes is different?
You cannot do average layout if the number of nodes is different.
Hi Eiko, thanks for this very useful tutorial, I actually managed to get it working after a few trials on my own data and got an almost perfect graph (i.e. in accord with my expectations) to “cluster” patients based on their methylome patterns. It is more informative or at least visually more pleasing than a “phylogenetic tree” approach. I am a total novice to R so please bear w/ me 🙂 But how do I delve into the details of this EGA? Specifically, I use identifiers like S102, S405, S250. I noticed that the EGA package shortens them “illegally”, so I am getting S40 and S25 for the last two id-s. How can I fix this, do you know? Thanks!
Hi Hedi, I’m glad this is useful to you. I actually don’t know EGA very well. Its benefit is that it’s really just one line of code, but the disadvantage is that there seem to be few things you can change at present.
What you could try is the following. EGA, under the hood, uses the qgraph package to estimate a gaussian graphical model (a regularized partial correlation network for metric data). You can probably get at the weighted adjacency matrix if you look into the object that EGA estimates. I don’t have R here at the moment, but if you look into the estimated EGA object in RStudio, there should be something like EGA$weiadj or so. You can then use qgraph to plot the network in a different way than EGA does. qgraph really gives you all the options.
e.g.
network_hedi <- qgraph(EGA$weiadj, xxx)Please also note that EGA assumes your data are metric, which is a big problem if you have binary data. In that case, you may want to use spinglass or walktrap and do a bit of magic in qgraph to color your nodes appropriately the way I did it in the tutorial.
You can find all the R-code I used to make the tutorial here.
There you can also find how I color the nodes manually in qgraph using the spinglass/walktrap algorithms. It's not pretty, and there are probably much better ways, but it will help you get your own network done.
Hi Eiko,
Thanks a lot. I did try this and got some error msg:
> network <- qgraph(EGA$weiadj, cormatrix)
Error in EGA$weiadj : object of type 'closure' is not subsettable
I guess I have to look more deeply into R in general. I am amazed how efficient it is!
Hi Hedi, thank you for your interest! To know more about how EGA works, and how accurate it is, give a look here: https://arxiv.org/abs/1605.02231. As Eiko pointed out, I am using qgraph + igraph. So, you can easily set up your node labels. Here we go:
ega1 <- EGA(yourdatahere, plot.EGA = TRUE)
#the glasso matrix is here:
ega1$glasso
#The "clusters" or dimensions of your data is here:
ega1$wc
So, you can use qgraph to adjust the lables as you want:
qgraph(ega1$glasso, layout = "spring", groups = as.factor(ega1$wc), labels = names(yourdatahere))
I hope it helps!
If not, please contact me here: hfgolino@gmail.com
Good luck,
Hudson
Thumbs up Hudson! Thanks!
Cheers, Eiko!
Hi Hudson, Thanks so much for taking the time to respond. The graphs look absolutely fabulous, I mean, as a method to split a network into subnetworks. I did indeed downloaded your paper but I know close to zero about matrix algebra. It is very impressive that you/others use such hard math in psychology, I had no idea. I’ll email you as I still try to get it right.
Hi Eiko & Hudson,
Just wanted to let you know that I finally succeeded with the labels, after studying a bit of R and reading up on glasso. So I had 8+6 columns, for 8 patients and 8 controls. After running EGA as suggested I created a list for each of the participants, as suggested in glasso.
> list1<- list("S1","s2","s3","s4","Samp5","s6","s7","s8","c9","c10","c11","c12","c13","c14")
#Using Hudson's suggestion about plotting the graph:
qgraph(ega$glasso, layout = "spring", groups = as.factor(ega$wc), labels = list1, vsize=9)
#This nicely plotted out the exact names, without abbreviation and increased the font size to 9. As the fog is thinning (in my brain) R is getting more fun! Thanks both 🙂
Hedi, n=16 does not sound like you have enough data to reliable estimate a network structure among multiple items — but maybe I misunderstand what you are doing here.
This is a good starting point for network stability: https://arxiv.org/abs/1604.08462
Hi Eiko, thanks for commenting. I actually have some 20000 rows (i.e. features, them being gene expression values in 15 individuals) and I want to estimate the network structure among the patients, i.e. how similar they are to each other. I got actually 2 subnetworks, i.e. 2 groups of patients/controls. Does this sound reasonable to you? Thanks for the link to the tutorial, I love them!
It does make sense, Hedi! However, as Eiko stated, it is necessary to pay attention to the stability of the dimensionality structure. That’s why I’m suggesting you to use the bootEGA algorithm, which is a bootstrap version of EGA!
That sounds exciting Hedi, what a huge dataset. I’d definitely consider looking at both correlation and regularized partial correlation networks in that case, both seem to provide some sort of interesting information in your case.
By the way, I’d love to see your results if you’re willing to share. Glad this methodology is applied to other fields, we usually model people as rows, you model them as columns.
Hi Eiko, I just generated both graphs (based on simple correlations and EGA). I’ll send them to you and Hudson by email. I have some qualms about justifying why the method works well on such cases but it does. I will appreciate your feedbacks!
Great, looking forward Hedi.
Hedi, I found some literature that may be interesting for you (clustering people similarly to what you are doing):
Karalunas, S. L., Fair, D., Musser, E. D., Aykes, K., Iyer, S. P., & Nigg, J. T. (2014). Subtyping Attention-Deficit/Hyperactivity Disorder Using Temperament Dimensions : Toward Biologically Based Nosologic Criteria. JAMA Psychiatry, 97239(9), 1015–1024. http://doi.org/10.1001/jamapsychiatry.2014.763
Hi Eiko,
Thanks for the article. In the meantime I wandered off from this topic a bit. Yesterday a paper of mine came out in Sci Rep, which also touches upon networks but in a rather naive way as I only wanted to show that a lot of genes relevant in schizophrenia correlate positively with synapse-related genes and negatively with myelin -related genes, i.e. the same gene set. I probably would it now differently, after reading your blog. Here is the paper: http://www.nature.com/articles/srep45494 What would be really interesting if your types of network of psychological features and gene networks could be combined to learn more about diseases. Which takes us to the genotype-phenotype problem, of course.
Hi Hedi, thanks for sharing your paper, and congratulations! I agree, using both psychological and biological variables into networks would be highly interesting, if you have data on that I’d be very curious to see what comes out of it. Will read your paper in more detail now.
Hi Eiko and thanks for the interesting and useful web blog.
I’m following your advice to set.seed() prior to using the spinglass.community command, but I’m not sure I’m doing it correctly. Shouldn’t I see a different computation and graphic output if I set a diffferent seed, because I’m noticing the same output regardless of seed.
rnorm(20)
set.seed(2)
rnorm(20)
#Now if we want the same random numbers
#we can just set the seed to the same thing
set.seed(2)
g = as.igraph(graph1, attributes=TRUE)
sgc <- spinglass.community(g)
Thanks, Rick
Hi Rick, thanks for the comment. In my case, graph1 was the network, estimated via:
library('qgraph')library('IsingFit')
library('bootnet')
library('igraph')
network1 <- estimateNetwork(data1, default="IsingFit")
graph1 <- plot(network1, layout="spring", cut=0, filetype="pdf", filename="network")
I then transferred the network into igraph and ran spinglass 100 times, each time changing the seed.
g = as.igraph(graph1, attributes=TRUE)matrix_spinglass <- matrix(NA, nrow=1,ncol=100)
for (i in 1:100) {
set.seed(i)
spinglass <- spinglass.community(g)
matrix_spinglass[1,i] <- max(spinglass$membership)
}
The results differed from each other, as you can see e.g. from the mean:
mean(as.vector(matrix_spinglass)) #5.87max(as.vector(matrix_spinglass)) #7
min(as.vector(matrix_spinglass)) #5
median(as.vector(matrix_spinglass)) #6
I think this is correct — if there are inconsistencies please do let me know.
Hi Eiko,
thank you for the tutorial, it is really intersting and helpful.
As I understood, there are several algorithms to detect communities within networks, beyond spinglass and walktrap.
Since results of the community detection algorithms vary slightly in my data set, I was wondering how to figure out which set of communities to interpret or how to deal with these results.
Do you think that modularity analysis (Newman & Girvan, 2014) could be an useful tool to evaluate the strength of communities within networks and thus to determine which community structure best fits the data?
Or do you know of any other data driven methods that could help to determine which community structure to interpret?
Thanks in advance!
Best,
Anna
Hi Anna, I’m really not an expert on community detection. The best source is in my opinion chapter 9 of the freely available network science book by Barabasi (http://barabasi.com/networksciencebook/).
I’ve often seen that spinglass and walktrap lead to somewhat different results (because they are based on different algorithms). Also, please be aware that spinglass can lead to different results if you repeat the procedure, so you should set a seed in R if you want your analyses to be reproducible (I usually run it 20 times and see if there are large differences, which can happen if the community detection is not very reliable).
Other than that, there has been very little work on the topic in psychology, and plenty of work in other fields, so they may be the best go-to source for now until we catch up. And in case you make progress, please don’t hesitate posting here, it’ll be very useful for many folks out there.
Thank you, Eiko!
That’s already helpful, I am reading the Barabasi’s book and looking for more valuable sources.
Pingback: The network approach to psychopathology: pitfalls, challenges, and future directions | Psych Networks
Hi.
thank you for this great post. It has been really helpful in determining the number of communities. I liked your advice on setting a different seed 100 times and choosing the median number of communities. Is there any way to cite you on that? Do you have a paper that could be cited as best practice?
Best, Lena
Hi Lena, I wouldn’t know where this is published. I’m honestly no expert in these techniques, and just played around with them a bit and discovered that spinglass is not determinant (the same way bootstrap isn’t) .. I’m sure everybody who actually works on communities knows this sort of thing. I know that Alexandre Heeren (Harvard) has looked into spinglass, but I don’t know exactly how he has worked with it. I’d write him an email, he’s friendly and very helpful.
Hi Eiko and Lena. First – thanks for the useful guide you’ve provided, these are really valuable contributions to the broader research community. Second, last year a colleague and I published a paper providing a method that can be used to quantify the robustness of the community detection. You can find it here: http://www.sciencedirect.com/science/article/pii/S0003347215004480
Hope it’s useful!
Damien
Thanks for sharing Damien, great resource!
Pingback: Network models do not replicate ... not. | Psych Networks
Pingback: A summary of my academic year 2017 – Eiko Fried
This is a great presentation of the problem, and the application seems relevant for numerous fields in my opinion; thanks for putting it up. I would love to use this code and cite you for the application of these tests for my own research. Unfortunately, in trying to work through this code, it throws an error almost immediately: calling the library “graph”, RStudio (currently running. 3.3) gives the following:
install.packages(“graph”)
Warning in install.packages :
package ‘graph’ is not available (for R version 3.3.3)
Other than a patch that runs an earlier version of R simultaneously, do you know of a work around for this? Thanks for any help you can give!
That’s qgraph, not graph. Thanks for flagging the mistake Jeremy, I will fix it asap.
Hi Eiko,
I have a question regarding the seed in the spinglass algorithm. To be more precise, you said you ran spinglass 100 times, got a median of 6 clusters and then used any seed which reproduces this median number of clusters. I am wondering, what if you had a quite large network and the solution you got wasn’t so stable (e.g. you got 6 clusters with different seeds but these differed in content). Would it be sensible to correlate memberships obtained with all the seeds that give this median number and then take a solution that has the biggest number of high correlations (e.g. >0.8) with other solutions ? It seems intuitive (as this solution would seem as the most stable one) but I’m not sure if I’m making any sense here.
Hi Anna, Marlene Werner and Donald Robinaugh have figured out a way to look into this further. We hope to provide an R tutorial soon that looks into the stability of the community solutions, and allows for a visualization of the stability.
As for choosing the one to plot, I think your idea is defensible: assuming instability, take the one that lies at the center of the multidimensional estimation space. I’m just not sure how to best find that (average distance in Euclidian space?), but correlations might be a promising start.
Hi, Anna. I came across the same problem when I use spinglass.
To solve the network stability problem, I ran spinglass for four times (My network is too big for more runs). I calculated the contingency table among all results and selected the meaningful intersection of all results. I lost a few false negative nodes in this way, but the core of each module will be relatively stable.
Thanks a lot for this tutorial. It helps a lot! I have a question about the spinglass clustering method. In my opinion, the output of spinglass relies on the input network, so it is important to make sure the input network is correct.
In your example, you used qgraph( graph = “cor”) to create a correlation network. I am wondering if there is any particular reason that you create a graph with qgraph instead of using functions in the igraph package, for example, “graph_from_adjacency_matrix()” function.
Hi Fuqi, I’m not very familiar with igraph and know qgraph very well (and have been teaching it for many years), so I use qgraph whenever I can simply for convenience sake. I know from others that igraph is incredibly broad and flexible, and I am sure other functions via igraph would work at least equally well.
Pingback: How to (not) interpret centrality values in network structures | Psych Networks
Many thanks for the great tutorial. I have been looking into doing a community analysis in R. From my reading of the literature, walktrap is one of the most reliable methods, as it can run on weighted networks – generating good results in various conditions e.g., sparse graphs, few clusters, etc. However, I was unsure if this method accounts for negative links, or simply puts these links to zero? Walktrap implemented in R does run on networks with negative links — but I saw that in the igraph library for C the documentation says that walktrap needs positive links & I found another peer-reviewed paper reiterating this (saying that it puts negative links to zero). But documentation in R does not state this (only that it takes weighted networks, with no mention of positive/negative links). I’m afraid that as an applied user the original walktrap publication does not illuminate things further for me. I know (from one of your other blogs 😉 that network analysis does not have a strong history of modelling negative weights e.g., only recently developing a centrality index “influence” which does account for these negative links – so I was not sure if walktrap was another expression of this.
So my question is does walktrap account for negative links or only set them to zero, and if the latter, how concerned should we be about this? Is it then for example preferable to revert to the spinglass method which definitely does account for negative links?
Thank you for your help!
Hi Felicity, I believe walktrap and spinglass take the absolute values of links, because they are only concerned with connectivity.
You can test this by taking a network with only positive edges, and estimate a community structure, and then change say on in three edges to negative, and estimate the community structure again. You should get identical communities.
Hi – Many thanks for the quick reply! I will look into this.
re: spinglass: I may be missing something, but but as far as I’m aware in igraph v1.0.1 the default is to use negative links only (for quicker computation etc), but via the “implementation” argument you can specify for it to take into account negative links.
Many thanks again!
Hi Hudson & Eiko:
I wonder if you are still being notified about/reading this blog? I used EGA again in rstudio, now successfully reading in an m * n table and EGA nicely clustered the ~ 200 patients, using data.frame as you (Hudson) suggested:
t <- as.data.frame(read.table(file= "table.txt", header=TRUE, sep="\t", row.names=1))
ega write(ega, file = “ega”)
Error in cat(list(…), file, sep, fill, labels, append) :
argument 1 (type ‘list’) cannot be handled by ‘cat’
Do you know of an easy solution to this?
Thanks,
Hedi
ps. resending it as my previous note was truncated somehow.
Again, my msg was truncated. Anyway, I could print the tabular output of (ega <- EGA::EGA(t) ) to the screen, however, when I want to save it to a file, with the command
write(ega, file = “ega”), the error msg appears:
Error in cat(list(…), file, sep, fill, labels, append) :
argument 1 (type ‘list’) cannot be handled by ‘cat’
What to do, any suggestion?
Thanks, Hedi
Hi Hedi, sorry for the late reply. Best to reach out directly to Hudson, I’ve also had some trouble recently with EGA but that was because they had recently implemented some new features that were sort of work in progress ;). I also plan to write an updated blog post on community detection this year together with Marlene Werner who has been working on bootstrapping methods for community detection (i.e. to assess the community’s stability); will keep you posted.
Any news on this or another package that let’s you do bootstrapping for community detection with the walktrap algorithm?
Yes, Marlene Werner, Donald Robinaugh, and me are currently working on a paper on the topic. The simulation part is largely done, writing this up will take a few more weeks at least though.
Alex Christensen and I just submitted a paper describing our bootEGA algorithm: https://www.researchgate.net/publication/331397573_Estimating_the_stability_of_the_number_of_factors_via_Bootstrap_Exploratory_Graph_Analysis_A_tutorial
This may be of interest to you all.
Also, the EGA package is now updated and stable (and hopefully will be available at CRAN soon).
Dear Eiko,
What a helpful tutorial and fantastic questions! I am hoping that this blog is still active, have two rather quick questions about the cluster_walktrap function (by Pons & Latapy, 2005). The input for this function seems to be in the form of a “graph”. Does this mean that I can use any model that suits my data (e.g., mgm) and enter the resulting graph in this function? See below my code to better explain. In addition, do you have any advice on how to interpret the modularity value of 0.24, which seems to be lower than desired and what was found previously (e.g., 0.48; Choi, 2017)?
#modeling mgm
mgmcom <- mgm(data, type = typecom, level = levelcom, lambdaSel = "EBIC")
graphcom <- qgraph(mgmcom$pairwise$wadj,
edge.color = manasmgmcom$pairwise$edgecolor,
layout = "spring", labels = myvar2, plot = TRUE )
#making the graph an igraph object
g = as.igraph(graphcom, attributes=TRUE)
#community detection
cluster_walktrap(g, weights = E(g)$weight, steps = 5, merges = TRUE, modularity = TRUE, membership = TRUE)
Many thanks!!!
Ceren
Hi Ceren,
We’re working on an updated blog on this, but the paper needs to be finished first 😉 ! Yes, I think you can use graph theoretical measures on any graph structure after you’ve estimated it. To what sense this is meaningful is an open question that goes beyond the modeling of course (e.g. see the recent preprint on ResearchGate by Laura Bringmann and colleagues on problems with the interpretation of betweenness centrality in psychological networks). I don’t know much about modularity unfortunately and would have to read up on that, too, sorry. Maybe contacted Karmel Choi who used it before? From memory, Barabasi discussed it in some detail in his free online network science book (http://networksciencebook.com/) which is usually a good source for these questions.
Cheers
Wonderful, and thank you for the resources! What I understand from Barabasi (was super helpful) is that positive modularity indicates a “potential community”, the subgraph likely has more links than expected by chance. My sense is that there is not a cut-off/rule of thumb, though Choi references Newman & Girman (2004) who reported that values for networks with strong community structure tend to range between 0.3 to 0.7…
I look forward to your blog & the paper!
Pingback: Tutorial: how to review psychopathology network papers | Psych Networks
Pingback: R tutorial: clique percolation to detect communities in networks | Psych Networks
Hello.
I am new in the field of network analysis and want to explore the idea of the Walktrap algorithm for my data. I fit the Ising models for my data, but now interested in examining the community showing the relationship between nodes. I am using the code underneath, but having warnings from R as:
“Error in igraph::cluster_walktrap(c, weights = c$weight, steps = 4, merges = TRUE, :
Not a graph object!”
Can you please help me with this.
Thanks in advance.
Pavneet Kaur
#read data
x1<-read.csv("random_full_no typ1_only types.csv")
Res2 <- IsingFit(x1,family='binomial',gamma = 0.25, plot=T, AND=F)
Graph_Ising2 <- qgraph(Res2$weiadj, layout = "spring", labels = colnames(x1))
Res2$weiadj
##############
#walktrap algorithm
library("igraph")
c<-Graph_Ising2$Edgelist
igraph::cluster_walktrap(c, weights = c$weight, steps = 4,merges = TRUE, modularity = TRUE)
Sorry it’s quite busy here so I don’t have the time to debug your code. You can try asking in our Facebook group Psychological Dynamics — it’s likely someone there has time to look at it. Your error message implies that igraph does not understand your object as network object.
https://www.facebook.com/groups/PsychologicalDynamics/
Thanks a lot Eiko Fried.
Hi Eiko,
Thank you for posting this tutorial! I have a very basic question regarding reading output that I’m hoping you can help me with. When interpreting output from Spinglass Community detection, how should the statement “omitted several groups/vertices” be interpreted? As you can see from my output 5 groups were detected, however, only 3 groups have nodes assigned to them. I have a feeling that I am missing something very basic here, any help would be appreciated!
Here is my input:
cluster_spinglass(graphPRA,
weights = NULL,
vertex = NULL,
implementation = c(“neg”))
And here is my output:
IGRAPH clustering spinglass, groups: 5, mod: 0.35
+ groups:
$`1`
[1] 1 5 11 12 15 18 24 27 28 33 35
$`2`
[1] 2 6 21 30 38 39
$`3`
[1] 3 8 14 16 20 25 36 37
$`4`
+ … omitted several groups/vertices
It seems like R abbreviates your output, right? So it’s probably about assessing the output. Maybe something like objectname$’4′ may work? In RStudio, if you save this as object and click on it, you can probably find it through that interface too.
Hi Eiko,
Thanks so much for this wonderful tutorial! I have a basic question: Is there any metric to quantify the ‘distance’ or ‘separability’ between communities in the network? I was thinking about using bootstrapping to estimate the stability of dimensions, but I wonder if there are any other measures available.
Thanks,
Han
Hi Han, I’m not sure of any established metrics and would probably have to do this “by hand”. You could e.g. look at all relations within a community compared to between communities or so.
Hi Han, We’ve done something similar to what you’re suggesting here: https://psyarxiv.com/9deay/
Also, there’s a way to compute the “distance” between communities using, for example, total correlation. See this paper here: https://www.tandfonline.com/doi/full/10.1080/00273171.2020.1779642
Nice tutorial!
Would it be possible, using these procedures, to group participants based on communities of items (i.e. something similar to what is done in latent class analysis or cluster analysis).
Cheers