Merlijn Olthof is a PhD student at the Behavioural Science Institute of Radboud University, Nijmegen, The Netherlands. His main research interest is the study of complexity in mental health with a particular focus on phase transitions and early-warning signals. Together with a project group – including his supervisors Anna Lichtwarck-Aschoff and Fred Hasselman – he recently published two preregistered studies on EWS and phase transitions in clinical change. In this blogpost, he addresses how EWS for clinical change can(not) be studied.
The concept of early-warning signals (EWS) for sudden shifts in the global behavior of complex systems received much attention after two review papers by Marten Scheffer and colleagues (Scheffer et al., 2009, 2012). These reviews illustrate how sudden qualitative changes (tipping points) in various complex systems are preceded by generic EWS1. For example, EWS have shown to precede tipping points in systems as diverse as the laser, the climate (e.g., the greenhouse-icehouse transition), and the brain (e.g., epileptic seizures). Clinical researchers have hypothesized that EWS and tipping points may also exist in mental health. Initial evidence for this idea was presented in a single-case study where EWS preceded relapse into depression. This shows that EWS are promising for personalized prediction in clinical practice.
The study of EWS for clinical change is, however, not straightforward. Many basic issues in this new field of research, such as how to define EWS in the context of clinical change, have not yet been addressed. In this blogpost, I address two very basic questions for the study of EWS for clinical change that kept me and my co-authors busy in preparation of our research. First, what are EWS? Second, how can we study EWS for clinical change? I end with some recommendations for EWS research and a brief summary of our recent study where we found that EWS have a real-time predictive value for sudden shifts in symptom severity.
What is an early-warning signal?
An early-warning signal is a within-system change in dynamics (indicative of critical fluctuations and/or critical slowing down) that is predictive of a phase transition.
This may not sound very sensible now, so let’s elaborate. Based on complex systems theories such as synergetics and catastrophe theory, two EWS can be distinguished: critical fluctuations and critical slowing down. Both indicate the rising instability in a system that precedes a phase transition (tipping point). This sounds abstract, but can be visualized intuitively (I hope you agree) by a ball rolling in a landscape with valleys and hills.
Consider the figure below which illustrates a simplified example of a phase transition that may occur in clinical change. At first, the system has only one stable state (an attractor) to which it will always return after a perturbation. This attractor state is visualized by a deep valley with steep hillsides. The behavior of the system is represented by the path of the ball. No matter where the ball is dropped in the most left landscape, it will very quickly settle in this attractor state. The system has a low return time to this attractor and can be said to be constrained: it has just a few degrees of freedom available to generate its behaviour. When this attractor landscape changes (middle part of the figure), the existing attractor is destabilized, which means that the system will now have more degrees of freedom available to generate its behaviour. This leads to increased variability of behaviour (i.e., critical fluctuations) and an increased time for the ball to return to the (now very shallow) valley, after it is dropped somewhere in the landscape. This increase in return time is called critical slowing down. After such a period of instability, the system re-stabilizes into a new attractor state, a process called self-organization (right part of the figure).

The example above highlights that EWS are not simply predictors of future events. Instead, they indicate the present instability in a system. Because this instability is often (but not always) followed by a phase transition, EWS are predictive.
Note that EWS are unspecific to the upcoming transition. Instability increases the probability of change (by increasing the degrees of freedom), but does not inform about the kind or direction of change when multiple new stable states are possible. This is why they are called generic EWS. Accordingly, our study found, in line with our hypothesis, that EWS predicted both sudden gains (transitions towards lower symptom severity) and sudden losses (transitions towards higher symptom severity).
How can we study EWS for clinical change?
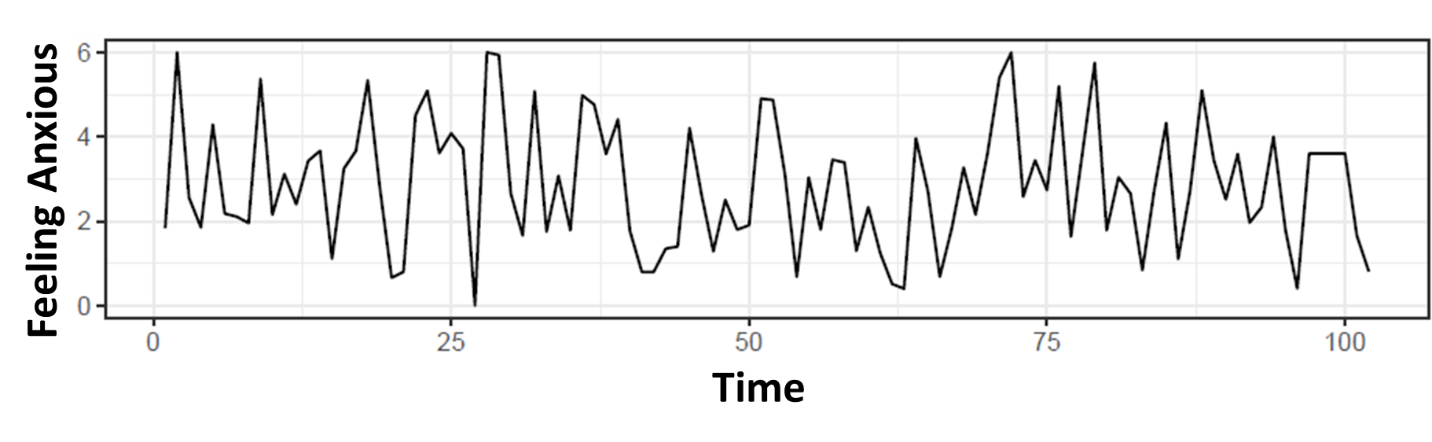
EWS are studied using time series analysis. A time series is a piece of intensive longitudinal data. For example, see the picture below. On the y-axis we see the scores on the item ‘I am feeling anxious’ for a hypothetical individual. On the x-axis we see the time. Different time series measures may be used as EWS. Variance, dynamic complexity and entropy have been used for critical fluctuations. Autocorrelation and variance have been used for critical slowing down. However, calculating such an EWS measure of a time series does not automatically mean that one is studying EWS. Three requirements can be formulated for the study of EWS.
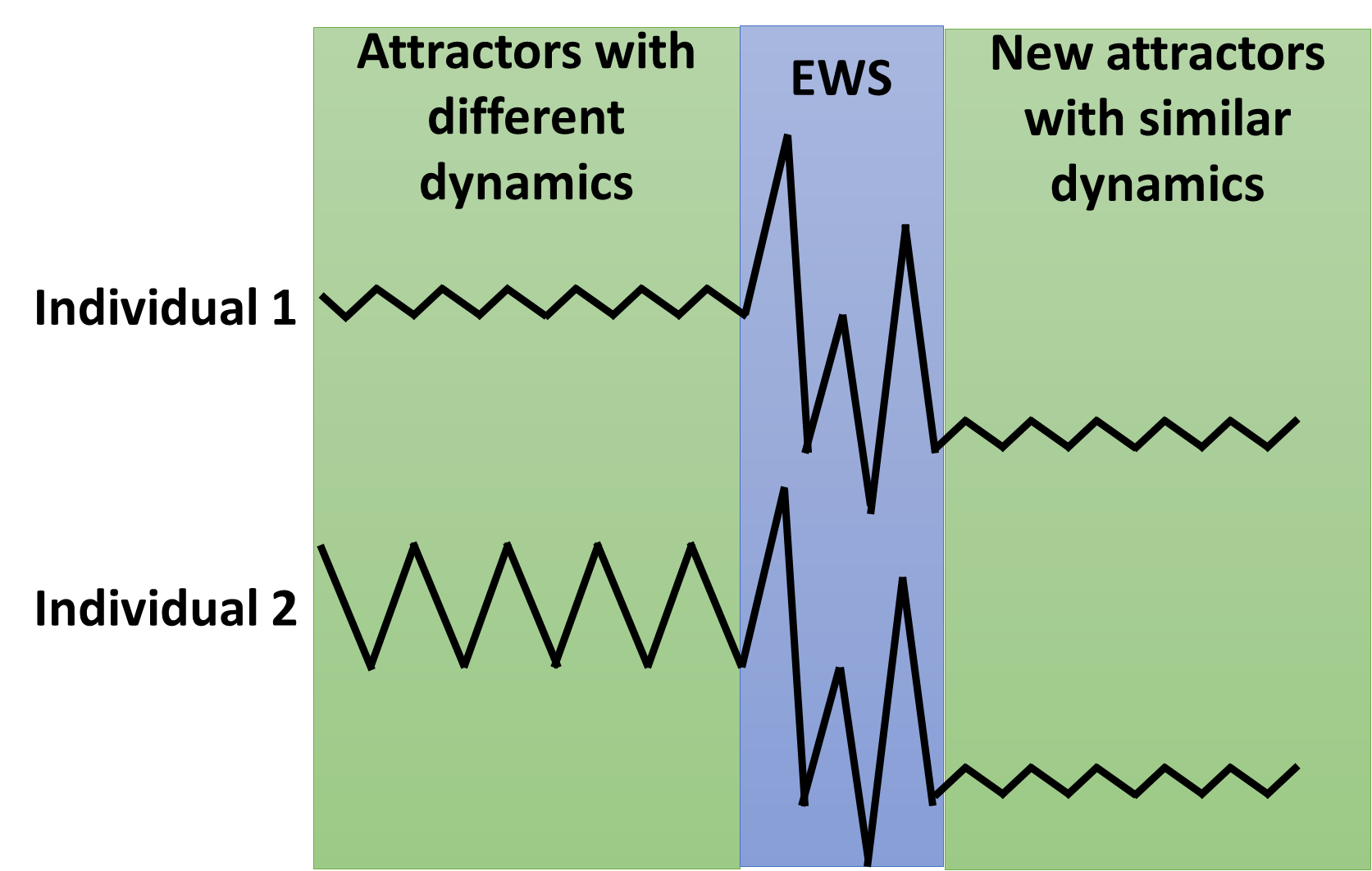
EWS can only be studied within-person
First, EWS describe a within-person process (the rise of instability over time) and can only be studied as such. Consider two persons who are entering psychotherapy for depression (see figure below). During a baseline measurement period preceding treatment, individual 1 has low variance in time series of daily self-ratings. Individual 2, in contrast, has high variance. Is the higher variance in individual 2 an EWS?
No. Between-person differences on measures used for EWS (e.g., variance) are in itself unrelated to EWS as is visualized in the figure below. The true EWS is the rise in instability over time within a system. So, it is not about the EWS measure (e.g. variance), but about the change in the measure over time. Only if we assume that individuals have exactly the same attractor landscape, which changes in an exactly similar way, leading to exactly similar behavior (i.e., ergodicity), between-person differences in dynamics can be used as EWS. But these conditions are never met as complex systems are per definition non-ergodic systems.
EWS should precede phase transitions
Second, EWS should warn for something. More specifically, they should warn for a phase transition. Again, this means that EWS can only be studied on the within-person level where phase transitions can be defined and predicted. When EWS are related to outcome while a phase transition is not defined, many alternative explanations for both the presence or absence of a relation exist. For example, symptom decrease might actually have preceded the EWS instead of the other way around. Or, patients might have improved within the same attractor state, in the absence of a phase transition. Or, EWS might have predicted symptom decrease in part of the sample, but increase in another part, leading to a null result. The relation between instability and treatment outcome is interesting to study, as findings suggest that successful therapies feature periods of instability. But we should avoid the term EWS when the specific transitions are unknown. The term ‘destabilization’, that is often used in psychotherapy research, seems more appropriate.
There should be periods of relative stability
Third, EWS should increase prior – and decrease after – the transition. In other words, there should be periods of relative stability before and after the phase transitions2.
EWS should be present shortly, as they indicate an instability in the system that cannot be maintained. But how short is short? That depends. A central issue in complex systems is that similar processes take place on multiple timescales. For example, in mental health we expect phase transitions in developmental time (e.g., onset of psychopathology), real-time (e.g., in emotional states, or even neuronal firing) and various in-between timescales (e.g., sudden gains in psychotherapy). In this regard, we can learn a lot from the dynamic systems approach to developmental psychology, which has a long tradition of dealing with different timescales (e.g., see this dynamic systems model for the development of anti-social behavior on multiple timescales). On a more practical note: we found that critical fluctuations in daily self-ratings were predictive a few days before a sudden gain/loss, but the optimal prediction window is an avenue for future research.
Eight recommendations for EWS research
With the requirements given above in mind, I present eight practical recommendations for the study of EWS for clinical change.
- Define the timescale of interest
Different types of phase transitions will occur at different timescales. It is important to have insight in this timescale for choosing an appropriate sampling rate (how frequent participants will have to complete self-ratings). Some transitions (e.g., recovery from depression) might be quite slow and daily or bi-daily sampling may be enough. Other transitions (e.g., aggression incidents) might be extremely fast, requiring more intensive sampling. For these ‘fast transitions’, physiological data may provide more suitable time series.
- Collect data during a change process
Researchers interested in EWS should collect data during a change process where phase transitions take place (for example, during psychotherapy). This makes EWS research fundamentally different from most contemporary idiographic research where it is recommended to collect data when change is absent (see this blogpost by Marilyn Piccirillo).
- Pinpoint the transition
The transition should be pinpointed in order to test the predictive value of EWS. Some transitions might be easier to pinpoint than others. Prime candidates are dramatic change events such as relapse in addiction, suicide attempts, and the onset of psychotic episodes. In repeated symptom severity measures, sudden gains and losses are also well-definable transitions. In experimental studies, sudden insight is a good example of a phase transition that can be predicted with EWS (e.g., see this study).
- Choose an appropriate measure of EWS
Autocorrelation and variance are very popular EWS measures, but they have limitations. Autocorrelation is an indirect measure of critical slowing down, as the real return times after perturbations are often unknown. This limits the interpretability, especially in clinical psychology where much is still unkown about the nature of attractors and perturbations. Measuring return time poses challenges, but it is something to strive for as it is the only way to obtain strong evidence that critical slowing down can be observed in clinical psychology. Variance also has limitations. It is sensitive to the mean, which is irrelevant for EWS and it does not take the time-ordering of variables into account. Entropy measures (e.g. permutation entropy), dynamic complexity, or recurrence quantification measures may be more suitable measures for critical fluctuations (many of these analyses are available in R-packages such as casnet).
- Perform a windowed analysis of EWS
When the transition is defined, EWS can be calculated. This is done through a windowed analysis. Make sure to use a backwards window. Only with a backwards window, the predictive value of EWS can be assessed. There is no informed standard for the window size, but a seven-day window may be used to control for weekend effects.
- First analyze, then aggregate
This advice given by Peter Molenaar is quoted in the amazing book The End of Average by Todd Rose. In line with the principles of idiographic science, transitions and EWS should be defined and calculated on an individual basis. Only after all individuals in a large dataset are analyzed, one can aggregate to test the predictive value of EWS by specifying a survival model. Multi-level modelling is essential in clinical change research as it allows to model individual differences. The multi-level survival model can handle different time series lengths, different timing of transitions and can include individuals with one transition, multiple transitions, or no transitions at all. Make sure to time-lag your predictors. This ensures that you really predict a transition in the future.
- Work transdisciplinary
This is a more broad recommendation, and quite obvious for everyone who is familiar with the work by Marten Scheffer and colleagues. But there is even more! For me it was very helpful to examine how EWS and phase transitions have been studied in other areas of science. Thanks to my supervisors and colleagues Fred Hasselman, Anna Lichtwarck-Aschoff and Maarten Wijnants, I got to read a lot of valuable ‘classics’ in movement science, cognition, development and psychotherapy research (for a list of my favourites see 3). Of course, especially in the natural science, there is a whole world of phase transition research to discover (for those not afraid of mathematics). I think the ‘complexity in mental health’ field can benefit from working transdisciplinary. This requires time effort, but in the end it will be efficient as we don’t waste our time to re-invent the wheel.
- Preregister your confirmatory study
Both confirmatory and exploratory research on EWS for clinical change are valuable and needed. But they should be clearly distinguishable. It is advisable to preregister confirmatory hypothesis tests for EWS given the large researcher degrees of freedom in defining transitions, choosing EWS and determining window sizes (for an example, you can find my preregistration on the osf).
Our study and outlook
Our recent study tested whether EWS were predictive of sudden gains and losses in psychotherapy for mood disorders in a large sample of patients. The study was set-up in line with the recommendations above. Patients completed daily self-ratings about their therapeutic process. For every patient, we pinpointed the phase transitions (sudden gains and losses) and calculated the EWS measures (dynamic complexity in our case) using a moving window analysis. Then, we tested the predictive power of EWS with a multi-level survival model. The findings are the first to show that EWS have a real-time predictive value for phase transitions in clinical change. Specifically, we found that an increase of 1 standard deviation in dynamic complexity values (a measure for critical fluctuations) was related to an 1.5 increased chance for a sudden gain or loss in the upcoming 4 days.
Our results show that EWS in daily self-ratings can potentially be used for real-time prediction of sudden gains and losses. In the future, it would be valuable to test whether we can also predict different clinical transitions, such as suicide attempts or relapse in addiction. Especially for these transitions, an early-warning system could be valuable for prevention. Another avenue for future research lies in the timing of interventions. Recall that EWS indicate an increase in the degrees of freedom available to a system, meaning that systems are more open to change when EWS are present. Psychological interventions might thus be more effective when timed during sensitive periods in which EWS are present.
Conclusion
The main message of this post is that an early-warning signal for clinical change is a within-person change in dynamics (indicative for critical fluctuations or critical slowing down) that is predictive of a phase transition. I hope that researchers interested in EWS find the post helpful and I look forward to more EWS research!
Merlijn Olthof
I wish to thank Fred Hasselman and Freek Oude Maatman for helpful suggestions and corrections for this blogpost. Also, I thank my co-authors – Fred Hasselman, Guido Strunk, Marieke van Rooij, Benjamin Aas, Marieke Helmich, Günter Schiepek and Anna Lichtwarck-Aschoff – for our cooperation on the EWS study.
- Note that in the behavioural and life sciences phase transitions and EWS have already been studied at least since the 1980’s, for example using catastrophe theory (e.g., Isnard & Zeeman, 1976; Jansen & van der Maas, 2001), synergetics (e.g., Haken, Kelso & Bunz, 1985; Thelen & Ulrich, 1991; Schiepek, 2003) and dynamic field theory (e.g., Thelen et al., 2001).
- Time series that show no relative stability but are also non-random do exist in complex systems: this is the phenomenon of chaos
- Hayes, A. M., Laurenceau, J. P., Feldman, G., Strauss, J. L., & Cardaciotto, L. (2007). Change is not always linear: The study of nonlinear and discontinuous patterns of change in psychotherapy. Clinical Psychology Review, 27(6), 715-723.
Kelso, J. A. S., Schöner, G., Scholz, J. P., & Haken, H. (1987). Phase-locked modes, phase transitions and component oscillators in biological motion. Physica Scripta, 35(1), 79.
Schmidt, R. C., Carello, C., & Turvey, M. T. (1990). Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. Journal of experimental psychology: human perception and performance, 16(2), 227.
Stephen, D. G., Dixon, J. A., & Isenhower, R. W. (2009). Dynamics of representational change: Entropy, action, and cognition. Journal of Experimental Psychology: Human Perception and Performance, 35(6), 1811.
Thelen, E., & Smith, L. B. (1994). A Dynamic Systems Approach to the Development of Cognition and Action.
Van Orden, G. C., Kloos, H., & Wallot, S. (2011). Living in the pink: Intentionality, wellbeing, and complexity. In Philosophy of complex systems (pp. 629-672).