This guest post was written by Joost Kruis (j.kruis@uva.nl) and summarizes the paper entitled “Three representations of the Ising model” published recently in Scientific Reports. Joost works in the Psychological Methods Department at the University of Amsterdam.
The first sentence of the ‘About’ section on this website (and for that matter of most scientific publications about psychological networks) mentioned the increasing popularity of the network perspective in social sciences. Statements such as these essentially describe the increasingly popular practice among researchers to explain associations, observed between measured variables, as a consequence of mutualistic relations between these variables themselves.
Examining the structure of observed associations between measured variables is an integral part in many branches of science. At face value, associations inform about a possible relation between two variables, yet contain no information about the nature and directions of these relations. This is captured in the (infamous) phrase about the quantity measuring the extent of the interdependence of variable quantities: correlation does not imply causation. Making causal inferences from associations requires the specification of a mechanism that explains the emergence of the associations.
In our paper we discuss three of these, theoretically very distinct, mechanisms and their prototypical statistical models. These three mechanisms, represented within the context of depression, are;
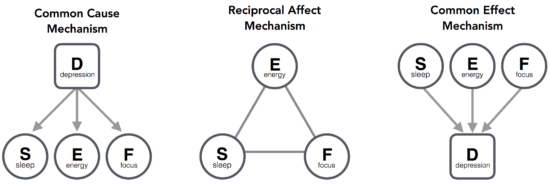
The first mechanism represents the (until recently most dominant) perspective on psychopathology where a mental disorder is viewed as the common cause of its symptoms. The common cause mechanism is statistically represented by the latent variable model, and explains the emergence of observed associations through an unobserved variable (depression) acting as a common cause with respect to the observed variables (sleep disturbances, loss of energy, concentration problems). The manifest variables (symptoms) are thus independent indicators of the latent variable (mental disorder) and reflect its current state.
The network perspective on psychopathology is captured by, what we in our paper term, the reciprocal affect mechanism. In this framework the associations between observed variables are explained as a consequence of mutualistic relations between these variables. In this framework the unobservable variable depression does not exist, but is merely a word used to describe particular collective states of a set of interacting features.
The third, common effect, mechanism explains associations between observed variables as arising from (unknowingly) conditioning on a common effect of these variables, and is statistically represented by a collider model. In this framework the observed variables act as a collective cause towards an effect. An example of this is receiving a depression diagnosis (effect) as a consequence of the occurrence of multiple symptoms (causes) that are linked by the DSM to the term depression.
While each of these mechanisms proposes a radically different explanation for the emergence of associations between a set of manifest variables. We demonstrate in the paper that their associated statistical models for binary data are mathematically equivalent. From this follows that, each of these three mechanisms is capable of generating the exact same observations, and as such that any set of associations between variables that is sufficiently described by a statistical model in one framework, can be explained as emerging from the mechanism represented by any of the three theoretical frameworks.
Having multiple possible interpretations for the same model allows for more plausible explanations when it comes to the theoretical concepts and the causal inferences we obtain from the measurement model applied to our data. Furthermore, the historical success of theoretically very implausible models, such as the latent variable model can, in retrospect, arguably be explained by the equivalence of these three models.
However, it also means that obtaining a sufficient fit for the statistical models in one of these frameworks is by no means evidence that it is the mechanism from this framework that actually generated the observations. That is, there will always exist representations from the other mechanisms that can explain our observations equally well.
We should thus not only apply a network model to our data because it gives us a pretty picture (which it does), but because we believe that the associations between the variables we have measured are explained as a consequence of mutualistic relations between these variables themselves.
Abstract
Statistical models that analyse (pairwise) relations between variables encompass assumptions about the underlying mechanism that generated the associations in the observed data. In the present paper we demonstrate that three Ising model representations exist that, although each proposes a distinct theoretical explanation for the observed associations, are mathematically equivalent. This equivalence allows the researcher to interpret the results of one model in three different ways. We illustrate the ramifications of this by discussing concepts that are conceived as problematic in their traditional explanation, yet when interpreted in the context of another explanation make immediate sense.
— Kruis, J. and Maris, G. Three representations of the Ising model. Sci. Rep. 6, 34175; doi: 10.1038/srep34175 (2016).
Pingback: The meaning of model equivalence: Network models, latent variables, and the theoretical space in between | Psych Networks
Pingback: Network models do not replicate ... not. | Psych Networks
Pingback: A summary of my academic year 2017 – Eiko Fried
Pingback: R tutorial: clique percolation to detect communities in networks | Psych Networks