In psychopathological networks, we often model ordinal items (problems or symptoms) that are not normally distributed, especially in general population samples. But if a variable shows a floor effect, meaning that the mean is close to 0, it often has a small variance, which in turn means that the variable cannot correlate strongly with other variables. An example is the item “paranoia” in a time-series study by Wigman et al. (2013):
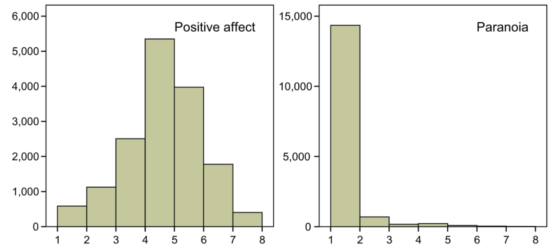
Differential variability
Differential variability — the phenomenon that items have drastically different variances such as positive affect and paranoia in the figure above — was brought up by one of the reviewers of my first published paper, and has stuck with me since. This is also the reason I mention this point in workshops, where I advise researchers to (1) always report both means and standard deviations of all their network variables in scientific papers, (2) and correlate the degree centrality of their nodes (the sum of absolute edges) with the standard deviation of their nodes. If the correlation is high, it means that differential variability of the nodes in the network may drive the centrality of the nodes (and hence the network structure).
The network below is an example. This is a symptom network estimated in a very large dataset (we’re submitting the paper soon so I won’t go into too much details). Node 2 (bottom right) is usually very highly connected with all other nodes for this disorder, but in our case, it’s only loosely connected. Why? Because the investigated population has extremely severe problems, and nearly everybody exhibits symptoms 2 in a very strong way. The variance of the item is much smaller than the variance of other items, which means it cannot exhibit strong connections with other items.
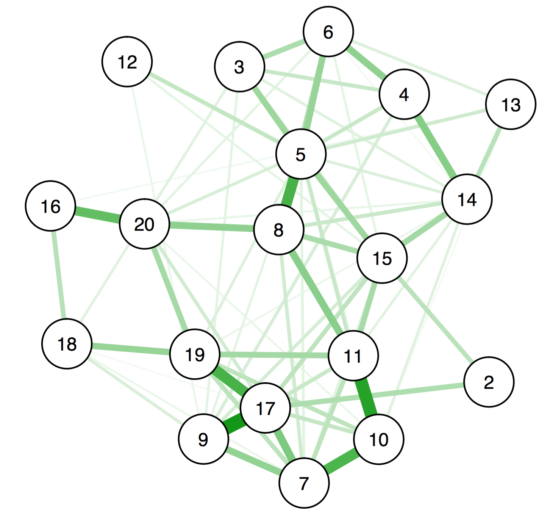
Terluin et al. 2016
A new paper published in PLOS ONE entitled “Differences in Connection Strength between Mental Symptoms Might Be Explained by Differences in Variance: Reanalysis of Network Data Did Not Confirm Staging” by Terluin, de Boer and de Vet tackles this issue in more detail now.
They correctly describe the problem as follows:
The strength of the connection between 2 variables (expressed as correlation or regression coefficient) rests principally on the amount of common (or shared) variance, relative to the total variance (i.e., common variance and unique variance including measurement error).However, the direct or indirect restriction of the variance of one or both variables (“range restriction”) reduces the connection strength [4]. The comparison of (sub)groups with different severity levels may result in different connection strengths between symptoms solely due to differences in variances [5]. Differential connection strength due to differences in variance is particularly a problem when psychological symptoms are studied in relatively healthy samples.
The authors re-analyzed data from a paper by Wigman et al. (2013) who estimated temporal networks using linear regressions which is can be problematic when variables are not normally distributed. Instead, Terluin and colleagues used inverse Gaussian regressions that assumes positively skewed data and thus can take into account differential variability of items. Their results differ from those of Wigman et al. (2013):
[our] alternative method failed to demonstrate increasing connection strength between mental states with increasing severity (i.e.,with increasing variance) in all models (except one) indicating that, when the skewness of the dependent variable was taken into account, no differential connection strength could be discerned across the severity subgroups.
While the authors note some limitations of their study, they are definitely correct in stating that differential variability impacts on the network structure and thus the interpretation of findings. Wigman and colleagues also wrote a reply and essentially agree with the main point, too.
I hope somebody will pick up this topic for a larger simulation study that could be a project for a good student. It would be great to know to what extent this is relevant, and how similar the variance among nodes should be to guarantee that it does not bias the estimation of the network structure. The paper predominantly discusses time-series network models, and I’m curious to which degree this is an issue in cross-sectional models as well. In Gaussian Graphical Models, the state-of-the-art regularized partial correlation networks for cross-sectional data, we first estimate the correlation matrix among variables based on the polychoric correlations in case of skewed ordinal data. I’m aware of an unpublished simulation study showing that the polychoric correlations perform reasonably well in large samples in case of skewed data, and lead to weak false positive associations in case of extreme skew, but it would be good to explore this on more detail. Note that you can also apply the nonparanormal transformation before you estimate the network, which may reduce skew. Finally, I’m curious to what degree this biases the estimation of factor models. If anybody knows literature on the topic, would you be so kind and share it in the comments below?
Here is the full abstract of Terluin et al. 2016:
Background. The network approach to psychopathology conceives mental disorders as sets of symptoms causally impacting on each other. The strengths of the connections between symptoms are key elements in the description of those symptom networks. Typically, the connections are analysed as linear associations (i.e., correlations or regression coefficients). However, there is insufficient awareness of the fact that differences in variance may account for differences in connection strength. Differences in variance frequently occur when subgroups are based on skewed data. An illustrative example is a study published in PLoS One (2013;8(3):e59559) that aimed to test the hypothesis that the development of psychopathology through “staging” was characterized by increasing connection strength between mental states. Three mental states (negative affect, positive affect, and paranoia) were studied in severity subgroups of a general population sample. The connection strength was found to increase with increasing severity in six of nine models. However, the method used (linear mixed modelling) is not suitable for skewed data.
Methods. We reanalysed the data using inverse Gaussian generalized linear mixed modelling, a method suited for positively skewed data (such as symptoms in the general population).
Results. The distribution of positive affect was normal, but the distributions of negative affect and paranoia were heavily skewed. The variance of the skewed variables increased with increasing severity. Reanalysis of the data did not confirm increasing connection strength, except for one of nine models.
Conclusions. Reanalysis of the data did not provide convincing evidence in support of staging as characterized by increasing connection strength between mental states. Network researchers should be aware that differences in connection strength between symptoms may be caused by differences in variances, in which case they should not be interpreted as differences in impact of one symptom on another symptom.
Terluin B., de Boer, M. R., de Vet, H. C. W. (2016). Differences in Connection Strength between Mental Symptoms Might Be Explained by Differences in Variance: Reanalysis of Network Data Did Not Confirm Staging. PLOS ONE 11(11): e0155205. doi: 10.1371/journal.pone.0155205
Update regarding the nonparanormal transformation
I mentioned the paranormal transformation above in case your data is skewed. As Sacha Epskamp pointed out with the example below, the nonparanormal transformation does not do much for you in case of highly skewed data with only few categories:
set.seed(1337)
DF <- data.frame(
x = c(rep(0,90),rep(1,10),rep(2,10)))
hist(DF$x)
library("huge")
DFnpn <- huge.npn(DF)
hist(DFnpn) |
Other options in this case are either to dichotomize your data and run an Ising Model, which should work unless you have very extreme skew, or estimate a Gaussian Graphical Model based on the polychoric correlations.
Hi! here you go -> http://www.apa.org/pubs/journals/features/met-a0030005.pdf
Thanks!
Pingback: Tutorial: how to review psychopathology network papers? | Psych Networks
Pingback: Network models do not replicate ... not. | Psych Networks
Pingback: A summary of my academic year 2017 – Eiko Fried
Pingback: How to (not) interpret centrality values in network structures | Psych Networks