This guest post was written by Giulio Costantini (costantinigiulio@gmail.com) who recently finished his PhD at the University of Milan Bicocca. His blog describes a new tutorial paper that was just published in Personality and Individual Differences (PDF), and follows his earlier 2015 tutorial paper on estimating psychological networks.
In a recently published paper on Personality and Individual Differences (Costantini et al., 2017), we provide a tutorial in R on new methods for estimating and analyzing personality and psychopathology networks. We focus on datasets that are often collected in psychology, but that are not often used to their full potential: Datasets including multiple groups and datasets including irregularly spaced repeated measures.
In personality and psychopathology research, it is relatively common to collect data on different groups of individuals (e.g., patients vs. controls, males and females, individuals assigned to different experimental conditions etc.). The patterns of similarities and differences among these groups are often particularly interesting. If one estimates a single network across groups (e.g., using graphical lasso; Friedman, Hastie, & Tibshirani, 2008), one completely loses track of inter-group differences. Conversely, if one estimates a separate network independently for each group, one does not exploit inter-group similarities to improve estimates. Furthermore, one cannot be sure whether the differences among the estimated networks reflect genuine differences or just small sampling fluctuations. We propose to jointly estimate networks in different groups using the Fused Graphical Lasso method (FGL; Danaher, Wang, & Witten, 2014), an extension of the graphical lasso algorithm that includes a lasso regularization on the differences of the parameters across groups. The FGL jointly estimates different networks across groups of individuals, by exploiting their similarities without masking their differences1.
In the case of irregularly spaced repeated measures, temporal networks (which encode cross-lagged relationships among variables; Bringmann et al., 2013) cannot be easily estimated. This is the case of event-contingent Ecological Momentary Assessment (EMA) data, in which the presentation of a questionnaire is connected to an event and not to a specific timing. This data-collection strategy typically results in participants filling the questionnaire in different moments and a different number of times. As discussed by Epskamp and colleagues (2017), repeated measures can be used not only to estimate temporal networks, but also contemporaneous and between-subject networks. Contemporaneous networks encode relationships among variables at the same timepoint, whereas between-subject networks encode involve stable differences among individuals. These types of networks can be both estimated even on irregularly-spaced repeated-measures data. Furthermore, one can use FGL to compute different between-subject networks and contemporaneous networks for each group.
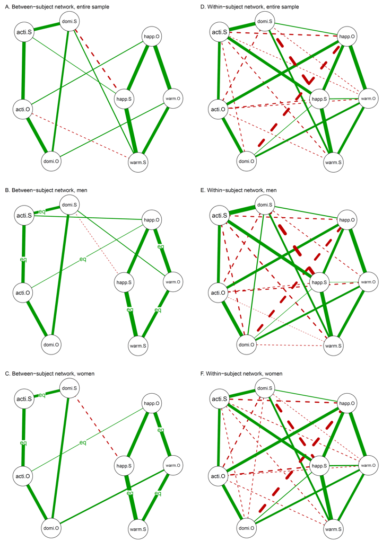
For our tutorial, we consider a dataset in which male and female participants filled in a questionnaire every time they experienced a significant social interaction (event-contingent EMA) and rated their behavior and emotions experienced during the interaction, as well as those of the other individual. We use package qgraph (Epskamp, Cramer, Waldorp, Schmittmann, & Borsboom, 2012) and a newly developed package that implements FGL, EstimateGroupNetwork (Costantini & Epskamp, 2017), to estimate between-subject and contemporaneous networks. We also discuss how such networks can be interpreted and what they can reveal about personality and psychopathology dynamics.
References
- Bringmann, L. F., Vissers, N., Wichers, M., Geschwind, N., Kuppens, P., Peeters, F., … Tuerlinckx, F. (2013). A Network approach to psychopathology: New insights into clinical longitudinal data. PLoS ONE, 8(4), e60188. http://doi.org/10.1371/journal.pone.0060188
- Costantini, G., & Epskamp, S. (2017). EstimateGroupNetwork: Perform the Joint Graphical Lasso and select tuning parameters. R package version 0.1.2.
- Costantini, G., Richetin, J., Preti, E., Casini, E., Epskamp, S., & Perugini, M. (2017). Stability and variability of personality networks. A tutorial on recent developments in network psychometrics. Personality and Individual Differences. http://doi.org/10.1016/j.paid.2017.06.011
- Danaher, P., Wang, P., & Witten, D. M. (2014). The joint graphical lasso for inverse covariance estimation across multiple classes. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 76(2), 373–397. http://doi.org/10.1111/rssb.12033
- Epskamp, S., Cramer, A. O. J., Waldorp, L. J., Schmittmann, V. D., & Borsboom, D. (2012). qgraph: Network visualizations of relationships in psychometric data. Journal of Statistical Software, 48(4), 1–18. http://doi.org/10.18637/jss.v048.i04
- Epskamp, S., Waldorp, L. J., Mõttus, R., & Borsboom, D. (2017). Discovering psychological dynamics: The gaussian graphical model in cross-sectional and time-series data. Retrieved from http://arxiv.org/abs/1609.04156v3
- Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432–441. http://doi.org/10.1093/biostatistics/kxm045
Footnotes
- Eiko speaking: For an empirical example in cross-sectional data, Giulio and I have recently used FGL in a large collaborative project to test how well PTSD networks replicate in 4 clinical datasets. This is one of the many examples where FGL might bring significant advances to the field.
This is such an excellent innovation! Regarding estimation, I was wondering about adaptive lasso versus glasso? I can’t seem to find what the differences are between these, nor how they perform against each other. In the “State of the aRt” paper, adaptive lasso is used, but it seems most papers since have begun using glasso. Could you help me understand why this is?
Hi Jonathan, there are many ways to estimate and regularize networks. I’m pretty sure I remember hearing Giulio Costantini and Sacha Epskamp talk about the adaptive lasso vs graphical lasso, and from I know these guys I’m pretty sure there are some simulation studies on which methods perform better under which circumstances. But I don’t think anything is published on that. I’d just write these 2 an email and ask (feel free to CC me, I’m curious about the answer).
Thanks for this latest development! Would FGL be appropriate to estimate two networks within one sample; i.e., if the goal were to compare the cross-sectional network structures of the self-report and interview versions of a scale given to a single group of participants?
Hi Pete, if my goal were to compare the network structures, I would use the NetworkComparisonTest R-package developed by Claudia van Borkulo at University of Amsterdam. The package is available on CRAN, the function is called NCT, and well documented.
Importantly, because you have the same population, you want to use the dependent version of the test (by specifying the argument ‘paired=TRUE’ in the NCT function).
Here is a paper that was accepted a few days ago in Schizophrenia Bulletin where we have a similar situation (the same people assessed in 2 days), and use the dependent version of the NCT.
Hope this helps!
Hi Pete,
You can still use FGL for estimating the networks, although FGL does not take advantage of the fact that the data were collected on the same sample. If your focus is on testing whether the two networks are equal or different, you can follow Eiko’s suggestion and use NCT.
Dear John,
I would suggest using graphical lasso, not much because of its performance (perhaps Sacha Epskamp has run a simulation on this, I remember that both behaved pretty well), but because its current implementation is more flexible, taking as input a correlation matrix without requiring the whole dataset, and even more importantly because it has been extended to the case of multiple groups.
Pingback: A summary of my academic year 2017 – Eiko Fried